前年圣诞节上,西班牙程序员Roman Cortes带来了用纯JavaScript脚本编写的神奇3D圣诞树,令人印象深刻。2月14日情人节就要来临了,还是Roman Cortes,这次他又带来了用JavaScript脚本编写的红色玫瑰花。用代码做出的玫瑰花,这才是牛逼程序员送给女友的最好情人节礼物呢!(提示:在不同浏览器下观看效果、速度会有很大的不同)
图片是由代码生成,用户可以刷新该页面,重复观看这朵玫瑰的呈现过程。

3D玫瑰花的实现代码如下:
<!DOCTYPE html>
<html>
<head>
<title>JavaScript和html53D玫瑰花(程序员的情人节礼物)</title>
<meta charset="utf-8">
</head>
<body>
<canvas id="c" height="500" width="500"></canvas>
<script>
var b = document.body;
var c = document.getElementsByTagName('canvas')[0];
var a = c.getContext('2d');
document.body.clientWidth;
</script>
<script>
// start of submission //
with(m=Math)C=cos,S=sin,P=pow,R=random;c.width=c.height=f=500;h=-250;function p(a,b,c){if(c>60)return[S(a*7)*(13+5/(.2+P(b*4,4)))-S(b)*50,b*f+50,625+C(a*7)*(13+5/(.2+P(b*4,4)))+b*400,a*1-b/2,a];A=a*2-1;B=b*2-1;if(A*A+B*B<1){if(c>37){n=(j=c&1)?6:4;o=.5/(a+.01)+C(b*125)*3-a*300;w=b*h;return[o*C(n)+w*S(n)+j*610-390,o*S(n)-w*C(n)+550-j*350,1180+C(B+A)*99-j*300,.4-a*.1+P(1-B*B,-h*6)*.15-a*b*.4+C(a+b)/5+P(C((o*(a+1)+(B>0?w:-w))/25),30)*.1*(1-B*B),o/1e3+.7-o*w*3e-6]}if(c>32){c=c*1.16-.15;o=a*45-20;w=b*b*h;z=o*S(c)+w*C(c)+620;return[o*C(c)-w*S(c),28+C(B*.5)*99-b*b*b*60-z/2-h,z,(b*b*.3+P((1-(A*A)),7)*.15+.3)*b,b*.7]}o=A*(2-b)*(80-c*2);w=99-C(A)*120-C(b)*(-h-c*4.9)+C(P(1-b,7))*50+c*2;z=o*S(c)+w*C(c)+700;return[o*C(c)-w*S(c),B*99-C(P(b, 7))*50-c/3-z/1.35+450,z,(1-b/1.2)*.9+a*.1, P((1-b),20)/4+.05]}}setInterval('for(i=0;i<1e4;i++)if(s=p(R(),R(),i%46/.74)){z=s[2];x=~~(s[0]*f/z-h);y=~~(s[1]*f/z-h);if(!m[q=y*f+x]|m[q]>z)m[q]=z,a.fillStyle="rgb("+~(s[3]*h)+","+~(s[4]*h)+","+~(s[3]*s[3]*-80)+")",a.fillRect(x,y,1,1)}',0)
// end of submission //
</script>
</body>
</html>
当然,感兴趣的人可以了解下面的实现过程与相关理论:
这朵三维代码玫瑰的呈现效果采用了蒙特卡罗方法,创造者对蒙特卡罗方法非常推崇,他表示在功能优化和采样方面,蒙特卡罗方法是“令人难以置信的强大工具”。关于蒙特卡罗方法可以参考:Monte Carlo method 。
具体操作:
外观采样呈现效果绘制
我用了多个不同的形状图来组成这朵代码玫瑰。共使用了31个形状:24个花瓣,4个萼片,2个叶子和1根花茎,其中每一个形状图都用代码进行描绘。
首先,来定义一个采样范围:
function surface(a, b) { // I'm using a and b as parameters ranging from 0 to 1.
return {
x: a*50,
y: b*50
};
// this surface will be a square of 50x50 units of size
}
然后,编写形状描绘代码:
var canvas = document.body.appendChild(document.createElement("canvas")),
context = canvas.getContext("2d"),
a, b, position;
// Now I'm going to sample the surface at .1 intervals for a and b parameters:
for (a = 0; a < 1; a += .1) {
for (b = 0; b < 1; b += .1) {
position = surface(a, b);
context.fillRect(position.x, position.y, 1, 1);
}
}
这时,看到的效果是这样的:
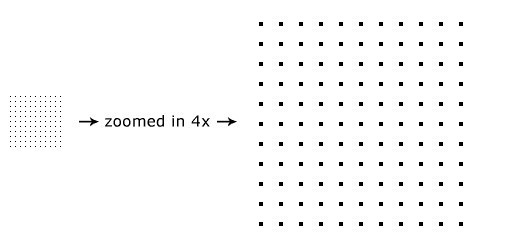
现在,尝试一下更密集的采样间隔:
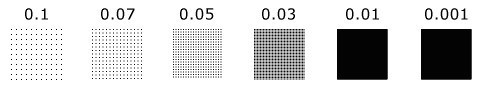
正如现在所看到的,因为采样间隔越来越密集,点越来越接近,到最高密度时,相邻点之间的距离小于一个像素,肉眼就看不到间隔(见0.01)。为了不造成太大的视觉差,再进一步缩小采样间隔,此时,绘制区已经填满(比较结果为0.01和0.001)。
接下来,我用这个公式来绘制一个圆形:(X-X0)^ 2 +(Y-Y0)^ 2 <半径^ 2,其中(X0,Y0)为圆心:
function surface(a, b) {
var x = a * 100,
y = b * 100,
radius = 50,
x0 = 50,
y0 = 50;
if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {
// inside the circle
return {
x: x,
y: y
};
} else {
// outside the circle
return null;
}
}
为了防止溢出,还要加上一个采样条件:
if (position = surface(a, b)) {
context.fillRect(position.x, position.y, 1, 1);
}
结果如下:

有不同的方法来定义一个圆,其中一些并不需要拒绝采样。我并无一定要使用哪一种来定义圆圈的意思,所以下面用另一种方法来定义一个圆:
function surface(a, b) {
// Circle using polar coordinates
var angle = a * Math.PI * 2,
radius = 50,
x0 = 50,
y0 = 50;
return {
x: Math.cos(angle) * radius * b + x0,
y: Math.sin(angle) * radius * b + y0
};
}
好了,现在让圆变形,以使它看起来更像是一个花瓣:
function surface(a, b) {
var x = a * 100,
y = b * 100,
radius = 50,
x0 = 50,
y0 = 50;
if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {
return {
x: x,
y: y * (1 + b) / 2 // deformation
};
} else {
return null;
}
}
结果:

这看起来已经很像一个玫瑰花瓣的形状了。在这里也可以试试通过修改一些函数数值,将会出现很多有趣的形状。
接下来应该给它添加色彩了:
function surface(a, b) {
var x = a * 100,
y = b * 100,
radius = 50,
x0 = 50,
y0 = 50;
if ((x - x0) * (x - x0) + (y - y0) * (y - y0) < radius * radius) {
return {
x: x,
y: y * (1 + b) / 2,
r: 100 + Math.floor((1 - b) * 155), // this will add a gradient
g: 50,
b: 50
};
} else {
return null;
}
}
for (a = 0; a < 1; a += .01) {
for (b = 0; b < 1; b += .001) {
if (point = surface(a, b)) {
context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
context.fillRect(point.x, point.y, 1, 1);
}
}
}
结果:

一片带色的花瓣就出现了。
3D曲面和透视投影
定义三维表面很简单,比如,来定义一个管状物体:
function surface(a, b) {
var angle = a * Math.PI * 2,
radius = 100,
length = 400;
return {
x: Math.cos(angle) * radius,
y: Math.sin(angle) * radius,
z: b * length - length / 2, // by subtracting length/2 I have centered the tube at (0, 0, 0)
r: 0,
g: Math.floor(b * 255),
b: 0
};
}
接着添加投影透视图,首先需要我们定义一个摄像头:
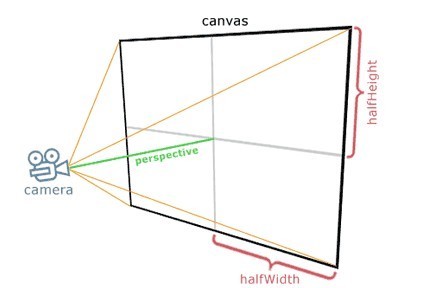
如上图,将摄像头放置在(0,0,Z)位置,画布在X / Y平面。投影到画布上的采样点为:
var pX, pY, // projected on canvas x and y coordinates
perspective = 350,
halfHeight = canvas.height / 2,
halfWidth = canvas.width / 2,
cameraZ = -700;
for (a = 0; a < 1; a += .001) {
for (b = 0; b < 1; b += .01) {
if (point = surface(a, b)) {
pX = (point.x * perspective) / (point.z - cameraZ) + halfWidth;
pY = (point.y * perspective) / (point.z - cameraZ) + halfHeight;
context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
context.fillRect(pX, pY, 1, 1);
}
}
}
效果为:

z-buffer
z-buffer在计算机图形学中是一个相当普遍的技术,在为物件进行着色时,执行“隐藏面消除”工作,使隐藏物件背后的部分就不会被显示出来。

上图是用z-buffer技术处理后的玫瑰。(可以看到已经具有立体感了)
代码如下:
var zBuffer = [], zBufferIndex;
for (a = 0; a < 1; a += .001) {
for (b = 0; b < 1; b += .01) {
if (point = surface(a, b)) {
pX = Math.floor((point.x * perspective) / (point.z - cameraZ) + halfWidth);
pY = Math.floor((point.y * perspective) / (point.z - cameraZ) + halfHeight);
zBufferIndex = pY * canvas.width + pX;
if ((typeof zBuffer[zBufferIndex] === "undefined") || (point.z < zBuffer[zBufferIndex])) {
zBuffer[zBufferIndex] = point.z;
context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
context.fillRect(pX, pY, 1, 1);
}
}
}
}
旋转
你可以使用任何矢量旋转的方法。在代码玫瑰的创建中,我使用的是欧拉旋转。现在将之前编写的管状物进行旋转,实现绕Y轴旋转:
function surface(a, b) {
var angle = a * Math.PI * 2,
radius = 100,
length = 400,
x = Math.cos(angle) * radius,
y = Math.sin(angle) * radius,
z = b * length - length / 2,
yAxisRotationAngle = -.4, // in radians!
rotatedX = x * Math.cos(yAxisRotationAngle) + z * Math.sin(yAxisRotationAngle),
rotatedZ = x * -Math.sin(yAxisRotationAngle) + z * Math.cos(yAxisRotationAngle);
return {
x : rotatedX,
y : y,
z : rotatedZ,
r : 0,
g : Math.floor(b * 255),
b : 0
};
}
效果:

蒙特卡罗方法
关于采样时间,间隔过大过小都会引起极差的视觉感受,所以,需要设置合理的采样间隔,这里使用蒙特卡罗方法。
var i;
window.setInterval(function() {
for (i = 0; i < 10000; i++) {
if (point = surface(Math.random(), Math.random())) {
pX = Math.floor((point.x * perspective) / (point.z - cameraZ) + halfWidth);
pY = Math.floor((point.y * perspective) / (point.z - cameraZ) + halfHeight);
zBufferIndex = pY * canvas.width + pX;
if ((typeof zBuffer[zBufferIndex] === "undefined") || (point.z < zBuffer[zBufferIndex])) {
zBuffer[zBufferIndex] = point.z;
context.fillStyle = "rgb(" + point.r + "," + point.g + "," + point.b + ")";
context.fillRect(pX, pY, 1, 1);
}
}
}
}, 0);
设置a和b为随机参数,用足够的采样完成表面填充。我每次绘制10000点,然后静待屏幕完成更新。
另外需要注意的是,如果随机数发生错误时,表面填充效果会出错。有些浏览器中,Math.random的执行是线性的,这就有可能导致表面填充效果出错。这时,就得使用类似Mersenne Twister(一种随机数算法)这样的东西去进行高质量的PRNG采样,从而避免错误的发生。
完成
为了使玫瑰的每个部分在同一时间完成并呈现,还需要添加一个功能,为每部分设置一个参数以返回值来进行同步。并用一个分段函数代表玫瑰的各个部分。比如在花瓣部分,我用旋转和变形来创建它们。
虽然表面采样方法是创建三维图形非常著名的、最古老的方法之一,但这种把蒙特卡罗、z-buffer加入到表面采样中的方法并不常见。对于现实生活场景的制作,这也许算不上很有创意,但它简易的代码实现和很小的体积仍令人满意。
希望这篇文章能激发计算机图形学爱好者来尝试不同的呈现方法,并从中获得乐趣。(Roman Cortes)