在本教程中，我们将在Scientific Linux下讨论矢量代数和相应的计算。 为了我们的目的，我选择了Python作为编程语言，其简单性和计算能力。 任何Linux发行版都默认使用通过终端窗口调用的Python编辑器/编译器。 我们来看一下矢量代数的一些概念。
注意： 我们只能在两三维的实际空间上工作 。
矢量代数
从数学的角度来看，向量空间的元素可以表示为属于该向量空间的多个元素的数组。 更具体地说，在数值计算方法中，它可以表示为实数列表 ，其具有三个基本特征：
大小
矢量的大小和代表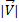 
;这是矢量的标量部分。 为了计算矢量的大小，我们必须执行下一个公式：
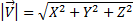
X，Y和Z是向量坐标。
方向
向量的方向由对于称为导向角的坐标系的每个轴具有特定角度的直线线给出。
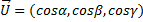
其中α ， β和γ是矢量导向角，它们的余弦是导子余弦，它们也可以通过将每个矢量坐标除以其大小来计算。
方向
两个方向之间的两个可能取向之一。
矢量代数和
为了形成向量的代数和，我们必须添加两个向量的同源坐标，参与代数和实数的相同属性。 如下：
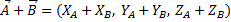
矢量的标量乘积
给定向量和标量，将标量的乘积向量定义为向量的每个坐标的标量积：
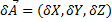
哪里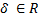 
单位向量
一个标量的产品向量的直接应用是单位向量 ， a 单位向量 是长度为1的规范向量。
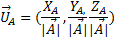
线性组合
当我们混合过去的操作，代数和和乘积向量标量时，我们得到一个线性组合，其中结果也是属于相同向量空间的向量，原样是：
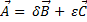
其中矢量A是矢量B和C的线性组合。
Python on Scientific Linux 7.1
为了实现向量代数，我们选择Python作为微积分语言。 我们选择的文本编辑器是gedit ，默认情况下与发行版Scientific Linux 7.1配合使用。
矢量的大小
让我们使用终端来拨打gedit ，或者点击应用程序选项卡上的图标：
首先，我们必须使用列表，作为代表向量，应该被声明为：
V=[2, 2, 1]
让我们声明一个变量来存储大小并给出一个值，我们使用0。
modV=0
现在我们使用类数学来操作平方根：
import math
计算量级：
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
我们可以看到，我们必须使用子索引从我们将要运行的列表中指定项目，从0开始。
完整的脚本如下：
V=[2, 2, 1]
modV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
print (modV)
一旦完成，我们必须保存扩展名为.py的文件，并找到文件路径，然后右键单击然后在终端窗口中打开一个终端窗口。 之后我们要调用python解释器键入：
$ python [path]/yourfilename.py
这将打开一个这样的窗口，并给出结果：
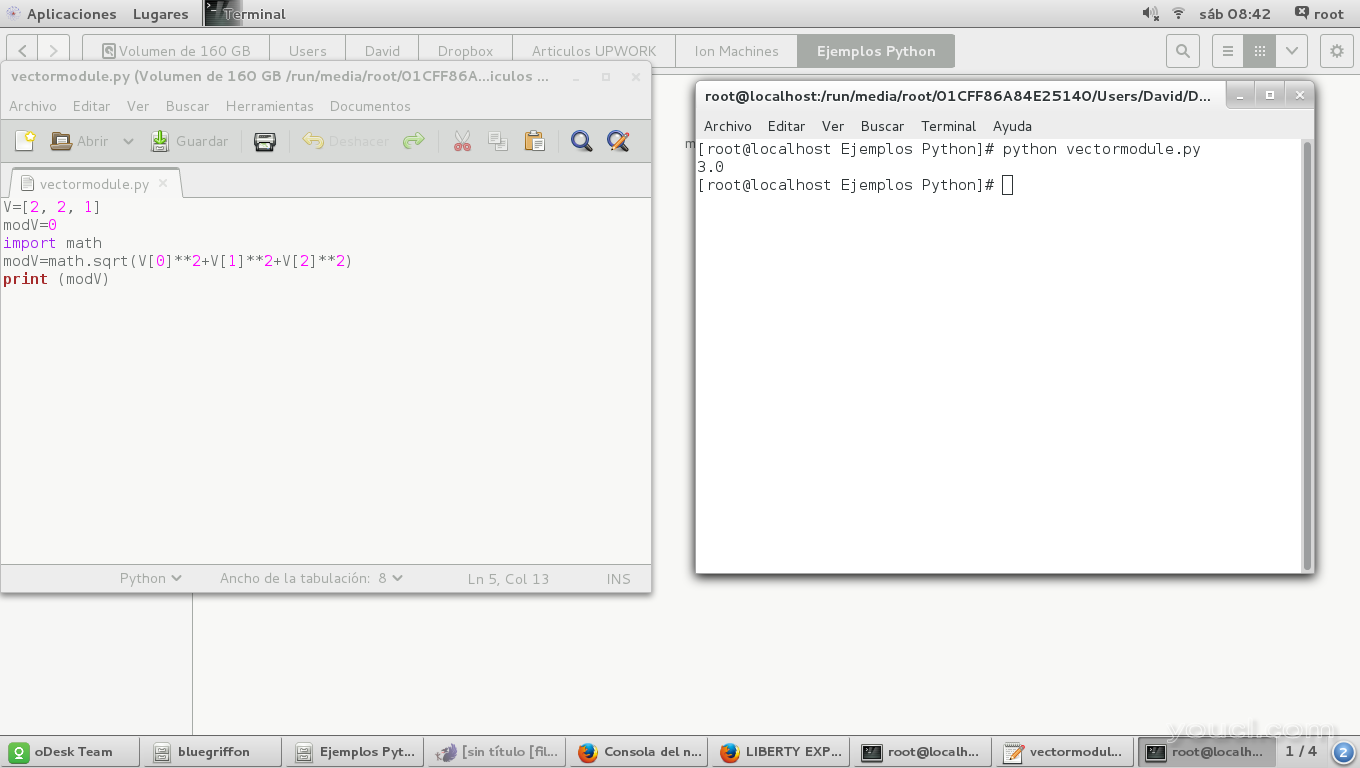
另一种方法是使用像这样的for循环：
for x in range (0,3):
modV+=V[x]**2
modV=math.sqrt(modV)
在这里，我们必须使用缩进技术，因为python解释器以这种方式工作。
向量的方向
使用课程数学
V=[2, 1, 2]
modV=0
import math
for x in range (0,3): #loop for calculating the magnitude
modV+=V[x]**2
modV=math.sqrt(modV)
for y in range (0,3): #loop for calculating the director cosines
V[y]=V[y]/modV
print (V)
结果是下一个：
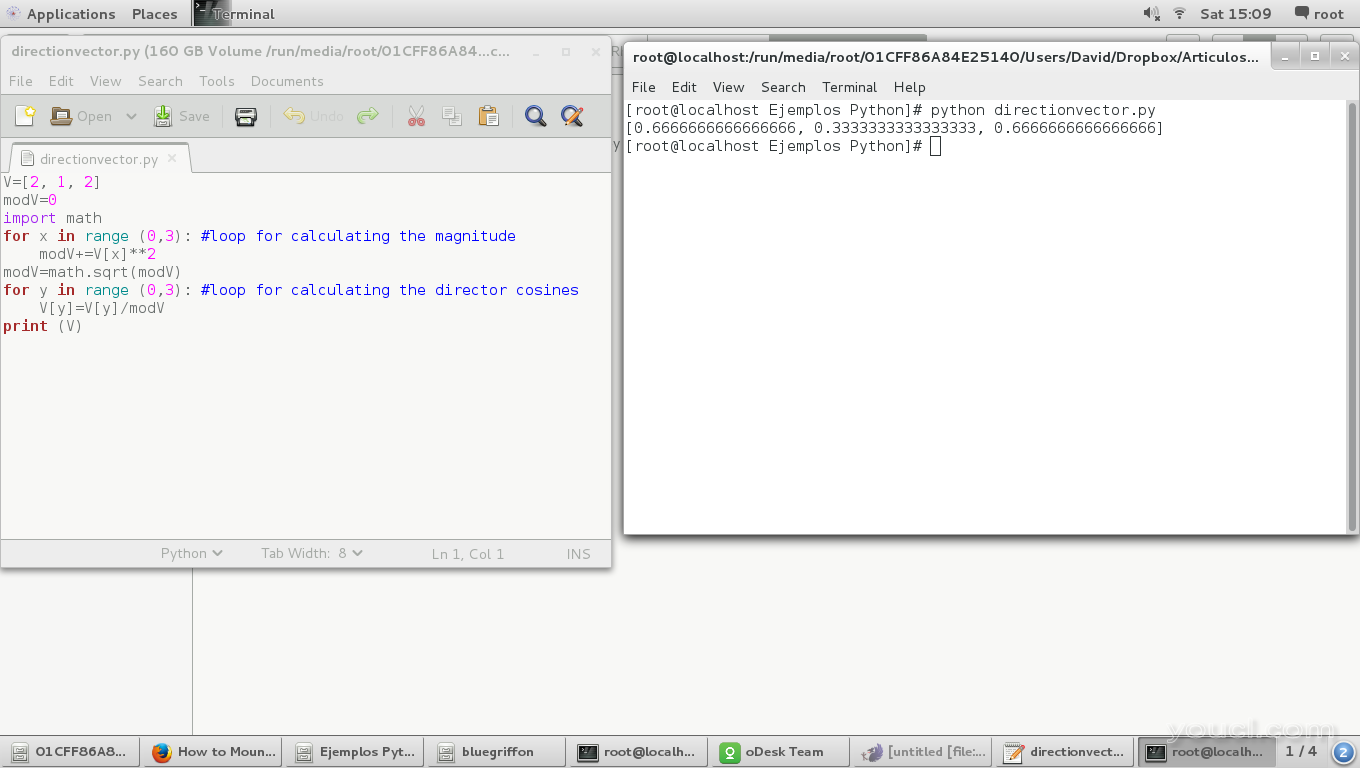
另一种做法是使用数学类的三角函数，就像这样：
首先让我们计算导演角度：
V=[2, 1, 2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))
然后让我们计算导演余弦并打印出来
for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
结果：
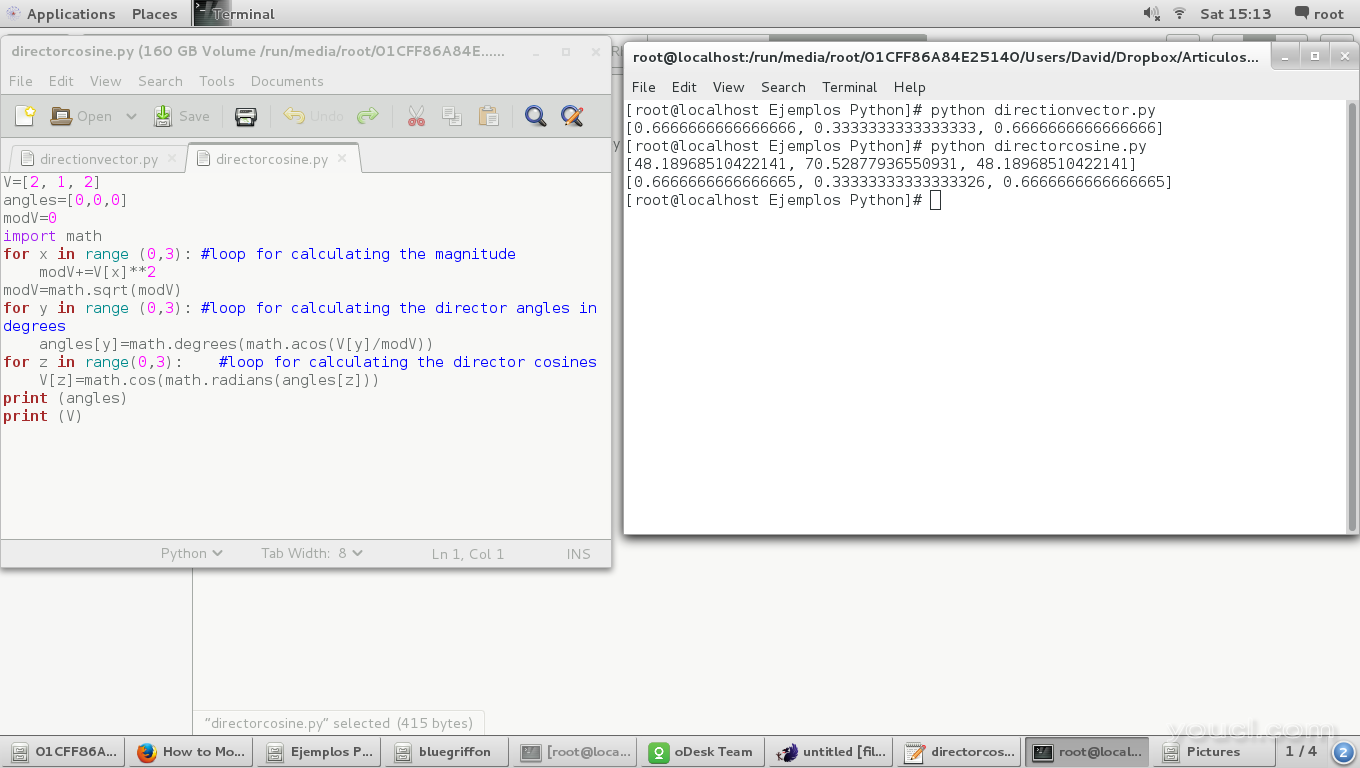
我们可以看到，导演余弦是相同的价值
向量的方向
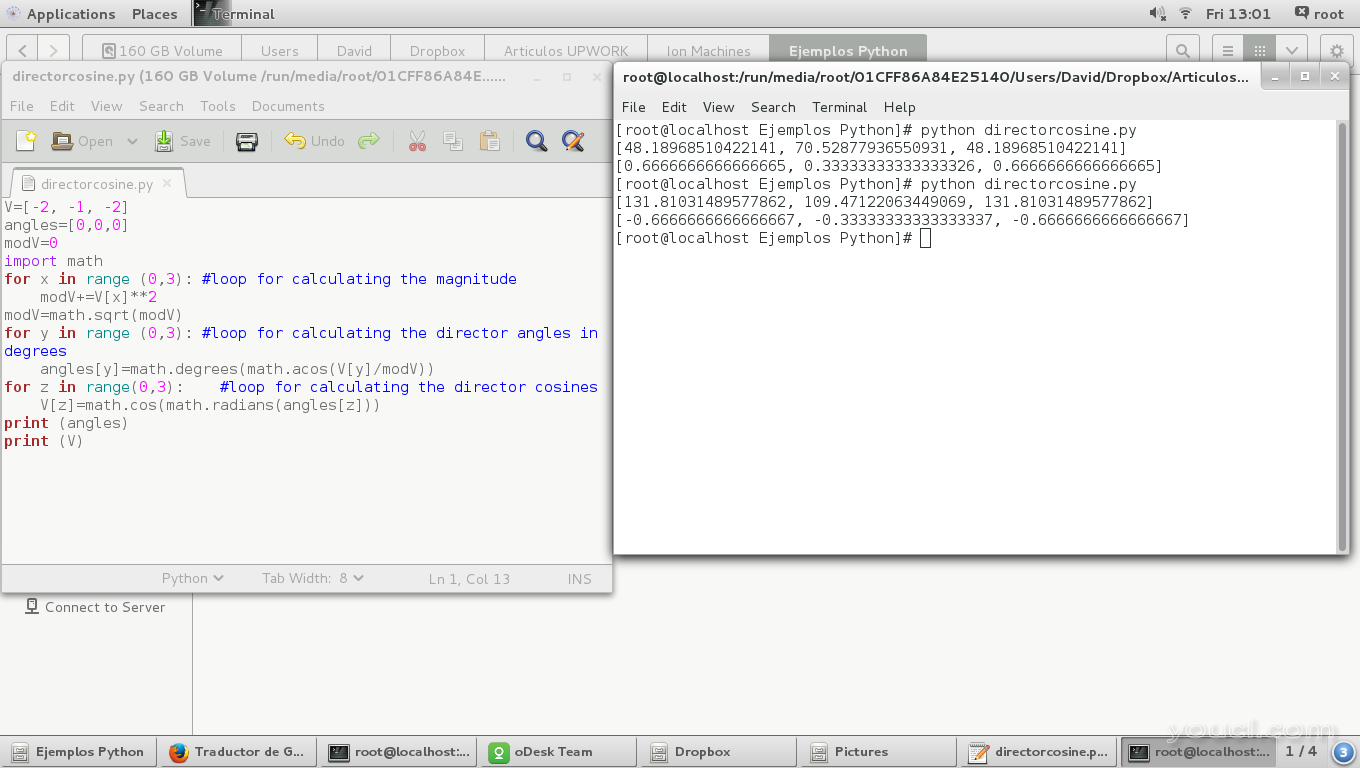
如果我们改变向量的所有坐标的符号，本质上，它们正在改变向量的方向：
V=[-2, -1, -2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
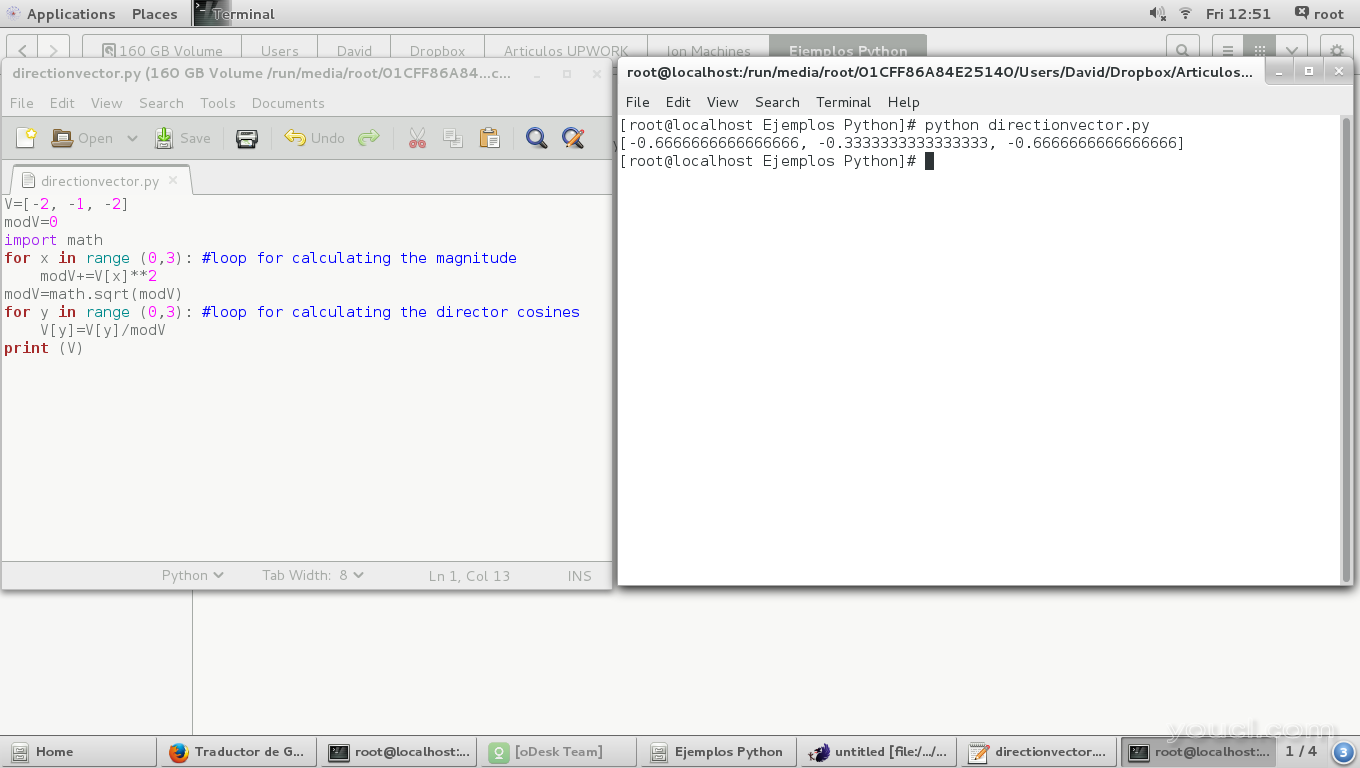
在下一张图像中，我们可以看到导向角与原稿的180度不同
矢量代数和
首先，我们必须声明所有涉及到代数和的向量，原因如下：
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
我们要总计A加B ，结果将存储在S中
在Python中添加两个向量（列表）相当于为结果向量的每个坐标运行一个'for'循环，所以我们必须做下一个：
for x in range(0,3):
S[x]=A[x]+B[x]
这里我们有代数向量和的完整脚本：
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
for x in range(0,3): #For loop for adding the homologue coordinate of each vector
S[x]=A[x]+B[x]
print 'S=',A, '+', B, '=', S
结果是：
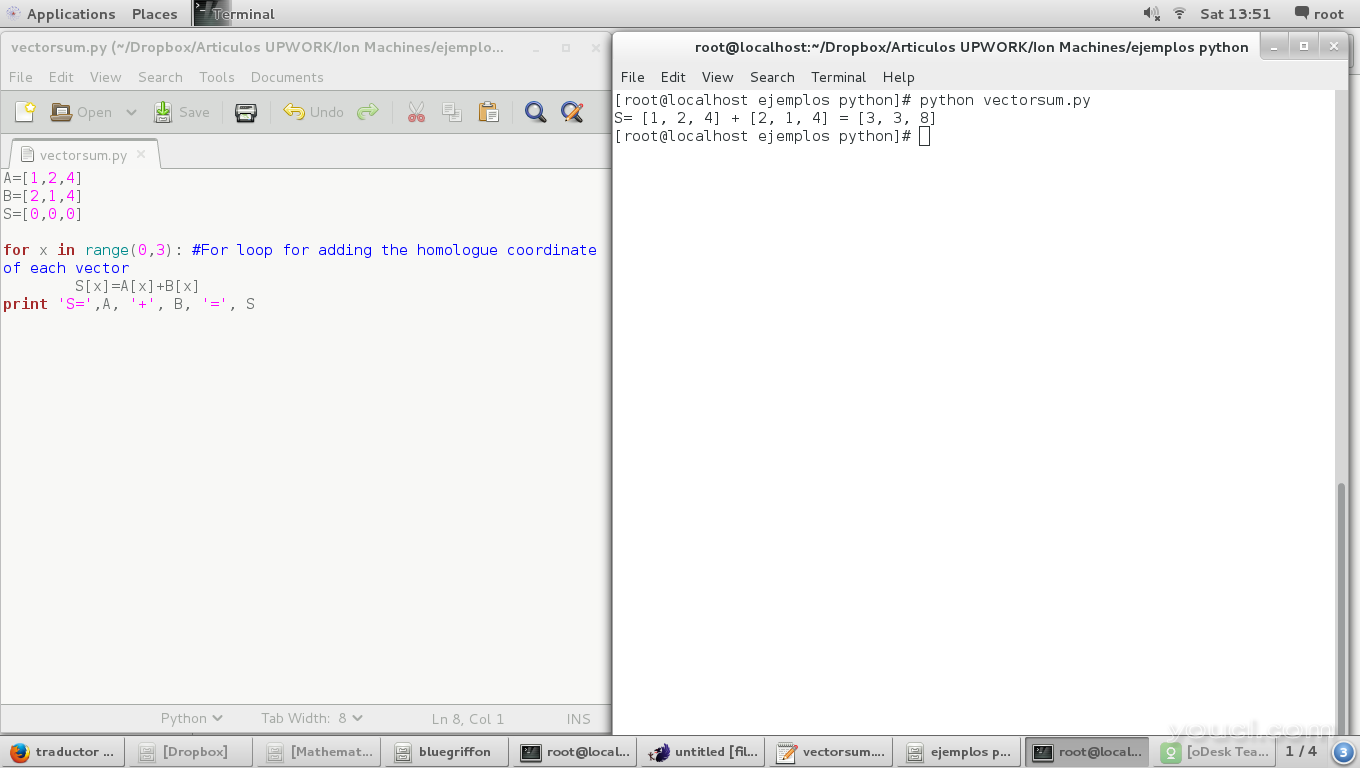
矢量的标量乘积
给定一个向量：
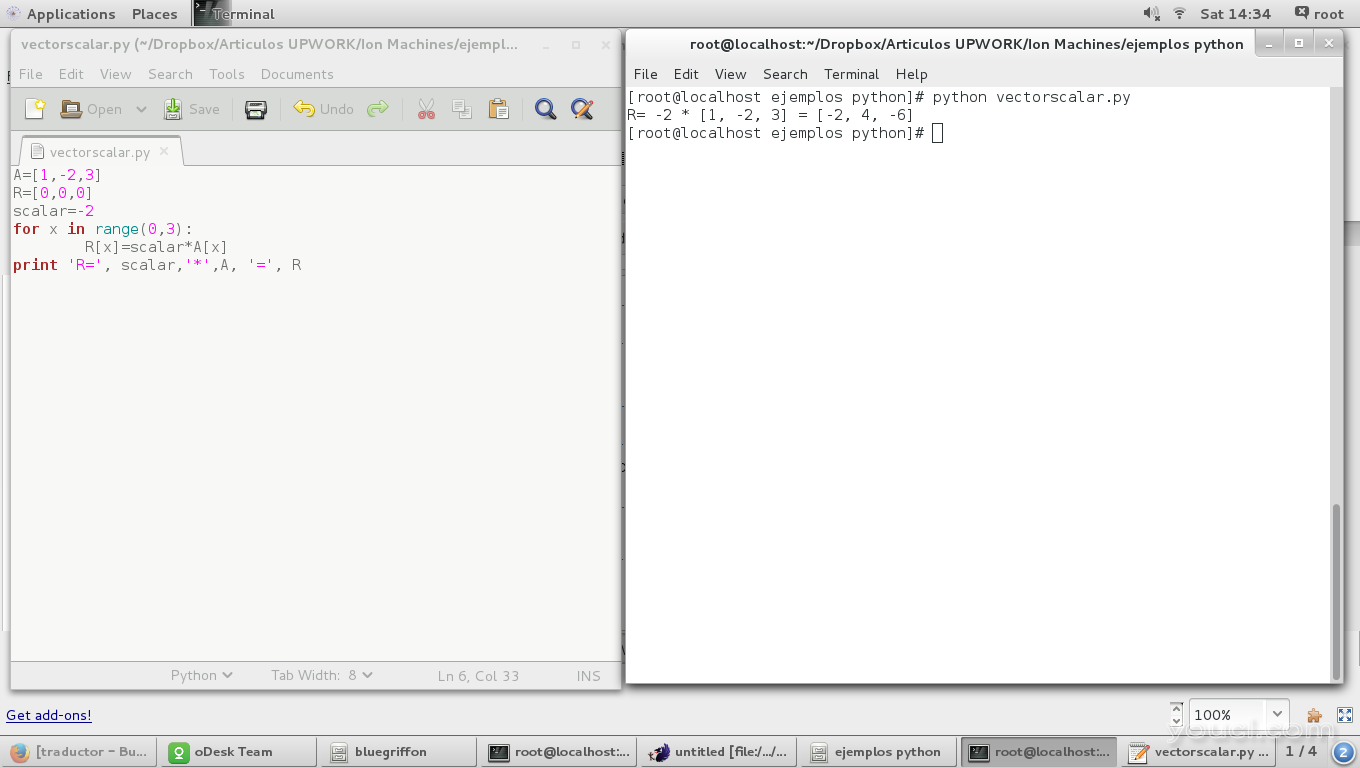
A=[1,-2,3]
和标量：
scalar=-2
标量的乘积向量定义为向量的每个坐标的标量积：
for x in range(0,3):
R[x]=scalar*A[x]
结果是：
单位向量
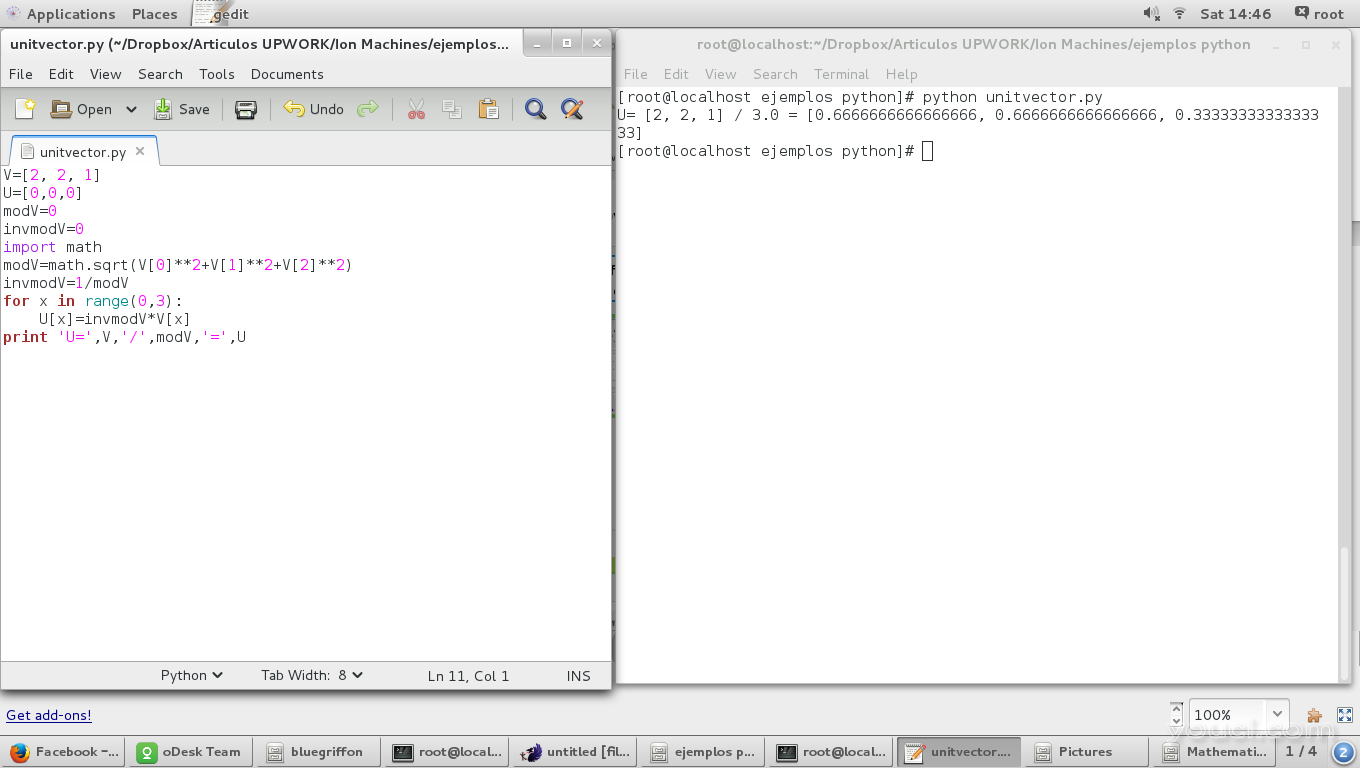
使用“矢量的大小”脚本我们有：
V=[2, 2, 1]
U=[0,0,0]
modV=0
invmodV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
invmodV=1/modV
for x in range(0,3):
U[x]=invmodV*V[x]
print 'U=',V,'/',modV,'=',U
结果是：
线性组合
给定三个向量A，B和C，我们可以分别计算乘以B和C的标量值，得到向量A.换句话说，将向量A作为向量B和C的线性组合：
A=[7, 9, -8]
B=[1, 3, -2]
C=[-2, 0, 1]
线性组合导致一个方程组，具有2个变量（标量）的3个方程，如果三个向量r3，或者如果它们是R3中的两个向量，则具有2个变量的2个方程，可以通过应用矩阵的行列式求解。 这里我们必须指出，由于Python处理的数据类型。 在许多情况下，当计算线性组合中涉及的标量时，结果将具有小数位，这将导致浮点运算。 由Python处理的数字数据类型是：Integer，Real，Long。 因此，我们必须将向量的坐标作为实数数据类型插入，因此这些代表实数（浮点数）。 我们必须了解并了解Python中数据类型的某些特性：
- Integer 占用 比 Real 类型 更少的 内存空间 。
- Real的操作比Integer更慢。
这里我们有相同的向量，但声明为真实类型：
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
所以，我们可以交换向量，从而始终有系统的解决方案。
我们必须做的第一个检查是关于矢量是否存在共面性，从而知道是否存在线性组合。 为此，我们将要执行一个行列式矩阵：
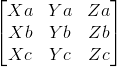
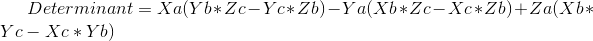
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
如果这个行列式等于零（0），则矢量之间存在线性依赖关系，我们可以继续计算标量。 如上所述，方程组具有三个具有两个变量的方程，产生一个确定的兼容系统，为此，我们必须采用三个方程中的两个，并求解标量值，然后检查第三个方程，如果前一个标量值解决它。 如果没有解决这个问题，那么就没有线性组合。
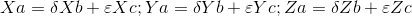
这里我们有完整的代码：
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
if det0==0:
det1=B[0]*C[1]-B[1]*C[0] #First Determinant involving the first and second lines of the equations system
if det1==0:
det2=B[1]*C[2]-B[2]*C[1] #Second Determinant involving the second and third lines of the equations system
if det2==0:
print 'Linear Combination Unexistent'
else:
det3=A[1]*C[2]-A[2]*C[1]
det4=B[1]*A[2]-B[2]*A[1]
sc1=det3/det2
sc2=det4/det2
if sc1*B[0]+sc2*C[0]==A[0]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
det3=A[0]*C[1]-A[1]*C[0]
det4=B[0]*A[1]-B[1]*A[0]
sc1=det3/det1
sc2=det4/det1
if sc1*B[2]+sc2*C[2]==A[2]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
print 'Linear Combination Unexistent'
结果：
[root@localhost ejemplos python]# python lincomb.py
Scalar 1 = 3.0 Scalar 2 = -2.0
[7.0, 9.0, -8.0] = 3.0 * [1.0, 3.0, -2.0] + -2.0 * [-2.0, 0.0, 1.0]
[root@localhost ejemplos python]#
总之，基本向量代数导致了一系列涉及线性方程组和/或实数的简单算术运算。 在另一个教程中，我们将看到我们如何开发带矢量的产品，如点产品，交叉产品或混合产品。
